08 - Modélisation - Classification

PRO1036 - Analyse de données scientifiques en R

Tim Bollé

November 10, 2025

Classification

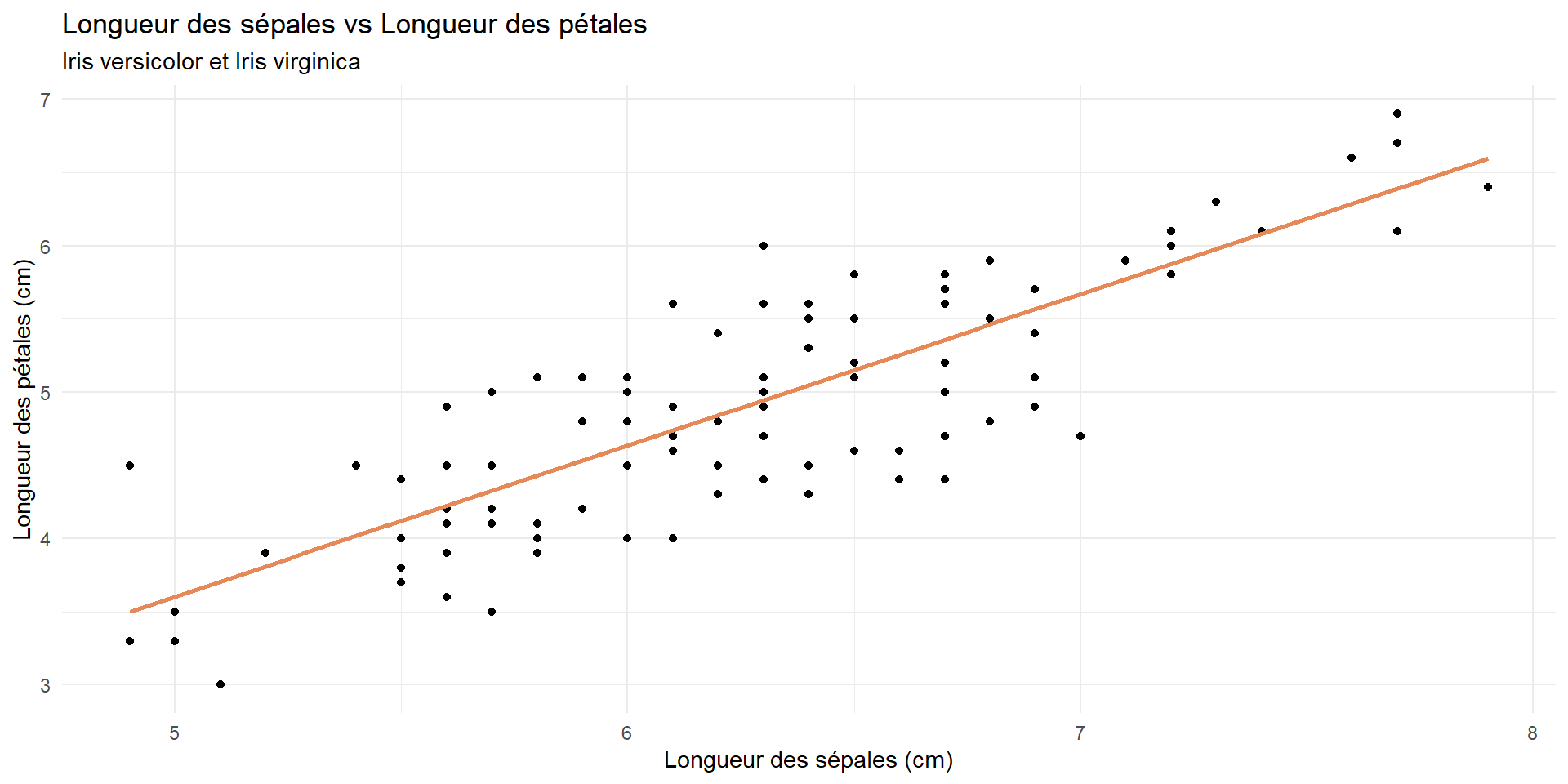
Problème avec la régression…

Cela fonctionne bien parce que nous avons une variable dépendante continue.

Graphe
Code

iris %>%
  filter(Species != "setosa") %>%
  ggplot(aes(x = Sepal.Length, y = Petal.Length)) +
  geom_point() +
  geom_smooth(method = "lm", color = "#E48957", se = FALSE) +
  labs(
    title = "Longueur des sépales vs Longueur des pétales",
    subtitle = "Iris versicolor et Iris virginica",
    x = "Longueur des sépales (cm)",
    y = "Longueur des pétales (cm)"
  ) +
  theme_minimal()

Mais si la variable dépendante est catégorielle ?

Graphe
Code

iris %>%
  filter(Species != "setosa") %>%
  mutate(
    Species_num = if_else(Species == "versicolor", 0, 1)  # conversion artificielle
  ) %>%
  ggplot(aes(x = Petal.Length, y = Species_num)) +
  geom_point(alpha = 0.7) +
  geom_smooth(method = "lm", se = FALSE, color = "#D81B60") +
  scale_y_continuous(
    breaks = c(0, 1),
    labels = c("versicolor", "virginica")   # remettre les étiquettes
  ) +
  labs(
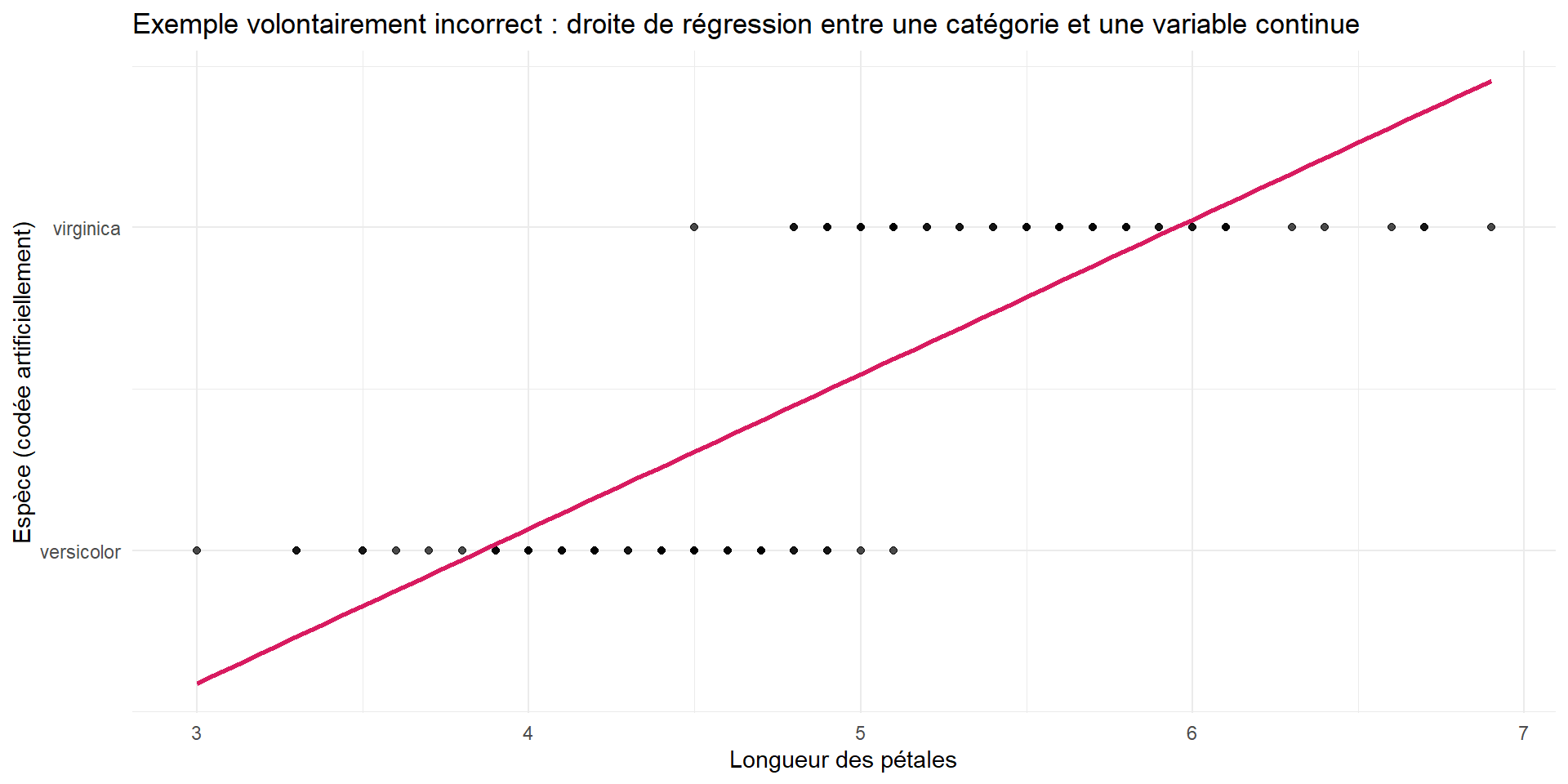
    title = "Exemple volontairement incorrect : droite de régression entre une catégorie et une variable continue",
    x = "Longueur des pétales",
    y = "Espèce (codée artificiellement)"
  ) +
  theme_minimal()

Pourquoi cela ne fonctionne pas ?

La variable dépendante est catégorielle (espèce de l’iris) et non continue.
Les valeurs prédites peuvent être en dehors des catégories possibles (par exemple, 0.5).
La relation entre la variable explicative et la variable dépendante n’est pas linéaire.
- \(Y\) ne suit pas une distribution normale.

Quelle solution ?

Prenons un peu de recul…

Les GML : Généralized Linear Models

Modèles linéaires généralisés

La régression linéaire est un cas particulier des modèles linéaires généralisés (GLM).
- La variable dépendante suit une distribution normale.

\[Y \sim \mathcal{N}(\mu, \sigma^2)\] Notre modèle permet d’estimer \(\mu\) en fonction des variables explicatives.

\[Y \sim \mathcal{N}(\beta_0 + \beta_1 X_1 + ... + \beta_p X_p, \sigma^2)\]

Visuellement

Les GML: Une généralisation

Les GML permettent de modéliser des variables dépendantes qui suivent différentes distributions (binomiale, Poisson, etc.).

Les GML: Une généralisation

Un GLM suit trois composantes principales : 1. Distribution de la variable dépendante: Spécifie la distribution statistique de la variable dépendante (ex: binomiale pour des données catégorielles, Poisson pour des données de comptage). - Cela nous diras comment la variance de la variable dépendante est liée à sa moyenne.

Un prédicteur linéaire: Une combinaison linéaire des variables explicatives \(\eta = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p\)
Fonction de lien: Relie la moyenne de la variable dépendante aux variables explicatives via une transformation spécifique.

\[g(\mu) = \eta = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p\]

Mathématiquement…

On cherche à estimer une valeur moyenne \(\mu\) de la variable dépendante \(Y\) en fonction de variables \(X\) (\(E(Y|X)\)).

\[ E(Y|X) = \mu \]

Comme \(Y\) ne suit pas une distribution normale, on utilise une fonction de lien \(g\) pour relier \(\mu\) au prédicteur linéaire :

\[ g(\mu) = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p \]

On a donc :

\[ E(Y|X) = \mu = g^{-1}(\beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p) \]

La fonction de lien

La fonction de lien permet de transformer la moyenne de la variable dépendante pour qu’elle puisse être modélisée par une combinaison linéaire des variables explicatives. En effet, une combinaison linéaire \(\eta = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p\) est généralement définie sur \(\mathbb{R}\) avec des valeurs pouvant aller de \(]-\infty;\infty+[\), contrairement à \(\mu\) qui ne peut pas toujours, dépendant de la loi que suit \(Y\)

Exemples de fonctions de lien courantes

Lien logit (pour les données binomiales/catégorielles) \[ g(\mu) = \log\left(\frac{\mu}{1 - \mu}\right) \]
Lien log (pour les données de comptage, Poisson) : \[ g(\mu) = \log(\mu) \]
Lien identité (pour les données normales) : \[ g(\mu) = \mu \]

La regession logistique

Classification binaire

Nous avions vu que la régression linéaire n’était pas adaptée pour modéliser une variable dépendante catégorielle.

Une première manière de voir les choses !

Nous pouvons transformer notre formule de la regression linéaire pour représenter le fait d’appartenir à une classe (0) ou l’autre (1)

\[ Y = \begin{cases} 1, & \text{si } \omega X \ge b, \\ 0, & \text{sinon}. \end{cases} \] où \(Y\) est la variable dépendante binaire, \(X\) est la variable explicative et où \(\omega\) et \(b\) permettent de régler le seuil de décision et le sens de la décision (est-ce que la classe 0 est à gauche ou à droite du seuil.

On peut réécrire cela avec notre formulation linéaire \(\eta = \beta_1 X + \beta_0\), en posant \(\omega = \beta_1\) et \(b = \beta_0\)

\[ Y = \begin{cases} 1, & \text{si } \beta_1 X + \beta_0 \ge 0, \\ 0, & \text{sinon}. \end{cases} \]

Visuellement

Regression logistique

La fonctione paliée n’est pas idéale pour des raisons d’optimisation. De plus, on souhaite obtenir des probabilités de classe plutôt que des décisions binaires strictes.

La fonction sigmoïde (logistique) est une alternative lisse qui mappe toute valeur réelle à l’intervalle [0, 1], ce qui est parfait pour modéliser des probabilités.

\[ S(z) = \frac{1}{1 + e^{-z}} \] Avec notre prédicteur linéaire \(\eta = \beta_0 + \beta_1 X\), la régression logistique modélise la probabilité que \(Y = 1\) comme suit :

\[ P(Y = 1 | X) = S(\eta) = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X)}} \]

Visuellement

Approche plus formelle…

La régression logistique est un type de modèle linéaire généralisé (GLM) adapté pour les variables dépendantes binaires.

Cela veut dire que notre variable dépendante \(Y\) suit une distribution binomiale : \[ Y \sim \text{Binomiale}(n=1, p) \]

où \(p\) est la probabilité que \(Y = 1\).

Approche plus formelle…

Nous cherchons à modéliser la probabilité \(p\) en fonction des variables explicatives via la fonction de lien logit :

\[ g(p) = \log\left(\frac{p}{1 - p}\right) = \beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p \] où \(g(p)\) est la fonction de lien logit, qui transforme la probabilité \(p\) en une échelle linéaire.

En regardant l’inverse de la fonction de lien, on obtient la probabilité \(p\) :

\[ p = \frac{1}{1 + e^{-(\beta_0 + \beta_1 X_1 + \cdots + \beta_p X_p)}} \]

En pratique

Modélisation

# Data
iris_filtered <- iris %>% 
  filter(Species != "setosa") %>%
  mutate(Species = factor(Species))

logistic_model <- logistic_reg() %>%
  set_engine("glm") %>% #Generalized Linear Model
  fit(Species ~ Petal.Length, data = iris_filtered, family = binomial) # On indique que la loi est binomiale

tidy(logistic_model)

# A tibble: 2 × 5
  term         estimate std.error statistic   p.value
  <chr>           <dbl>     <dbl>     <dbl>     <dbl>
1 (Intercept)    -43.8      11.1      -3.94 0.0000812
2 Petal.Length     9.00      2.28      3.94 0.0000804

Qualité du modèle

Pour mesurer la qualité du modèele, on ne peut pas utiliser le R² comme pour la régression linéaire. On utilise plutôt des métriques adaptées pour la classification binaire.

Table de confusion :

	Réel : Classe 0	Réel : Classe 1
Prédit : Classe 0	Vrai Négatif (TN)	Faux Négatif (FN)
Prédit : Classe 1	Faux Positif (FP)	Vrai Positif (TP)

Les Faux Positifs (FP) constituent des erreurs de type I, tandis que les Faux Négatifs (FN) représentent des erreurs de type II.

Qualité du modèle

Il est ensuite possible de calculer des métriques

Sensibilité : \(P(\hat{Y}=1 \mid Y=1) = \frac{TP}{TP + FN} = 1-FNR\)
Spécificité : \(P(\hat{Y}=0 \mid Y=0) = \frac{TN}{TN + FP} = 1-FPR\)

où \(FNR\) est le taux de faux négatifs et \(FPR\) le taux de faux positifs.

Prédiction

Faire des prédictions

Souvent on souhaite utiliser un modèle ajusté pour faire des prédictions sur de nouvelles données. On peut le faire en régression et en classification

Principe est simple:

On met les valeurs des variables explicatives d’une nouvelle observation dans le modèle
Le modèle calcule la valeur prédite de la variable dépendante

En pratique c’est un peu plus compliqué:

Nous ne sommes pas sûrs que le modèle est bon
Nous ne sommes pas sûrs que les nouvelles données sont similaires aux données d’entraînement

Underfitting et Overfitting

Séparation des données

Entraînement vs Test

Jeu d’entraînement:
- Utilisé pour ajuster le modèle
- Majorité des données (généralement 80%)
Jeu de test:
- Utilisé pour évaluer la performance du modèle ajusté
- Important de ne pas l’utiliser pendant l’ajustement du modèle
- Reste des données (généralement 20%)

L’idée est de mesurer la performance du modèle sur des données que le modèle n’a jamais vues auparavant.

En pratique

# Il y a un tirage aléatoire dans la séparation des données
# En fixant un seed, on s'assure d'obtenir toujours la même séparation - Reproductibilité 
set.seed(1116)
# Séparer les données en deux ensembles (80% entraînement, 20% test):
iris_split <- initial_split(iris_filtered, prop = 0.80)
# Création des jeux d'entraînement et de test
train_data <- training(iris_split)
test_data  <- testing(iris_split)

Ce que ça donne

glimpse(train_data)

Rows: 80
Columns: 5
$ Sepal.Length <dbl> 6.3, 7.7, 7.2, 6.1, 6.9, 5.5, 6.0, 6.3, 5.6, 6.3, 7.7, 5.…
$ Sepal.Width  <dbl> 3.4, 2.8, 3.2, 2.8, 3.1, 2.6, 2.2, 2.5, 3.0, 2.8, 2.6, 3.…
$ Petal.Length <dbl> 5.6, 6.7, 6.0, 4.0, 5.1, 4.4, 4.0, 4.9, 4.5, 5.1, 6.9, 4.…
$ Petal.Width  <dbl> 2.4, 2.0, 1.8, 1.3, 2.3, 1.2, 1.0, 1.5, 1.5, 1.5, 2.3, 1.…
$ Species      <fct> virginica, virginica, virginica, versicolor, virginica, v…

glimpse(test_data)

Rows: 20
Columns: 5
$ Sepal.Length <dbl> 7.0, 6.9, 5.5, 5.7, 6.3, 6.6, 6.1, 6.7, 5.4, 6.0, 5.6, 5.…
$ Sepal.Width  <dbl> 3.2, 3.1, 2.3, 2.8, 3.3, 2.9, 2.9, 3.1, 3.0, 3.4, 2.7, 2.…
$ Petal.Length <dbl> 4.7, 4.9, 4.0, 4.5, 4.7, 4.6, 4.7, 4.4, 4.5, 4.5, 4.2, 3.…
$ Petal.Width  <dbl> 1.4, 1.5, 1.3, 1.3, 1.6, 1.3, 1.4, 1.4, 1.5, 1.6, 1.3, 1.…
$ Species      <fct> versicolor, versicolor, versicolor, versicolor, versicolo…

Entraînement du modèle

iris_fit <- logistic_reg() %>%
  set_engine("glm") %>%
  fit(Species ~ . , data = train_data, family = binomial) # on utilise toutes les variables explicatives

tidy(iris_fit)

# A tibble: 5 × 5
  term         estimate std.error statistic p.value
  <chr>           <dbl>     <dbl>     <dbl>   <dbl>
1 (Intercept)    -41.9      26.3      -1.59  0.111 
2 Sepal.Length    -2.46      2.39     -1.03  0.303 
3 Sepal.Width     -6.56      4.58     -1.43  0.152 
4 Petal.Length     9.31      4.80      1.94  0.0521
5 Petal.Width     18.0      10.0       1.80  0.0726

Prédictions sur le jeu de test

predict(iris_fit, test_data)

# A tibble: 20 × 1
   .pred_class
   <fct>      
 1 versicolor 
 2 versicolor 
 3 versicolor 
 4 versicolor 
 5 versicolor 
 6 versicolor 
 7 versicolor 
 8 versicolor 
 9 versicolor 
10 versicolor 
11 versicolor 
12 versicolor 
13 versicolor 
14 virginica  
15 virginica  
16 virginica  
17 virginica  
18 virginica  
19 virginica  
20 virginica

Prédictions avec probabilités

iris_pred <- predict(iris_fit, test_data, type = "prob") %>%
  bind_cols(test_data %>% select(Species))

iris_pred

# A tibble: 20 × 3
   .pred_versicolor .pred_virginica Species   
              <dbl>           <dbl> <fct>     
 1        1.000e+ 0       1.36 e- 5 versicolor
 2        9.99 e- 1       1.31 e- 3 versicolor
 3        1.000e+ 0       4.94 e- 5 versicolor
 4        1.000e+ 0       1.19 e- 4 versicolor
 5        9.99 e- 1       1.45 e- 3 versicolor
 6        1.000e+ 0       1.71 e- 5 versicolor
 7        9.99 e- 1       8.98 e- 4 versicolor
 8        1.000e+ 0       3.37 e- 6 versicolor
 9        9.98 e- 1       2.45 e- 3 versicolor
10        1.000e+ 0       2.45 e- 4 versicolor
11        1.000e+ 0       1.80 e- 5 versicolor
12        1.000e+ 0       8.79 e-11 versicolor
13        1.000e+ 0       2.87 e- 6 versicolor
14        3.52 e-10       1.000e+ 0 virginica 
15        1.20 e- 6       1.000e+ 0 virginica 
16        2.90 e- 4       1.000e+ 0 virginica 
17        3.76 e- 5       1.000e+ 0 virginica 
18        2.49 e- 3       9.98 e- 1 virginica 
19        6.37 e- 8       1.000e+ 0 virginica 
20        1.12 e- 3       9.99 e- 1 virginica

matrices de confusion

cm <- predict(iris_fit, test_data) %>%
  bind_cols(test_data %>% select(Species)) %>%
  conf_mat(truth = Species, estimate = .pred_class)

cm

            Truth
Prediction   versicolor virginica
  versicolor         13         0
  virginica           0         7

Le tableau rendu par la fonction predict dépend de si on souhaite avoir la classe prédite ou bien la probabilité pour chaque classe (type = "prob").

Selon ce que l’on souhaite faire après, il faut utiliser l’une ou l’autre.

Comparaison

logistic_reg() %>%
  set_engine("glm") %>%
  fit(Species ~ Sepal.Width, data = train_data, family = binomial) %>%
  predict(test_data) %>%
  bind_cols(test_data %>% select(Species)) %>%
  conf_mat(truth = Species, estimate = .pred_class)

            Truth
Prediction   versicolor virginica
  versicolor          3         2
  virginica          10         5

logistic_reg() %>%
  set_engine("glm") %>%
  fit(Species ~ Sepal.Length, data = train_data, family = binomial) %>%
  predict(test_data) %>%
  bind_cols(test_data %>% select(Species)) %>%
  conf_mat(truth = Species, estimate = .pred_class)

            Truth
Prediction   versicolor virginica
  versicolor          8         1
  virginica           5         6

Courbes ROC

Les Courbes ROC (Receiver Operating Characteristic) sont utilisées pour évaluer la performance des modèles de classification binaire de manière visuelle en représentant le taux de vrais positifs (sensibilité) en fonction du taux de faux positifs (1-spécificté)

iris_pred %>%
  roc_curve(
    truth = Species,
    .pred_versicolor
  ) %>%
  autoplot()

Courbes ROC - Comparaison

logistic_reg() %>%
  set_engine("glm") %>%
  fit(Species ~ Sepal.Width, data = train_data, family = binomial) %>%
  predict(test_data, type="prob") %>% # Il nous faut les probabilités
  bind_cols(test_data %>% select(Species)) %>%
  roc_curve(
    truth = Species,
    .pred_versicolor
  ) %>%
  autoplot()

logistic_reg() %>%
  set_engine("glm") %>%
  fit(Species ~ Sepal.Length, data = train_data, family = binomial) %>%
  predict(test_data, type="prob") %>%
  bind_cols(test_data %>% select(Species)) %>%
  roc_curve(
    truth = Species,
    .pred_versicolor
  ) %>%
  autoplot()

08 - Modélisation - Classification

Classification

Problème avec la régression…

Mais si la variable dépendante est catégorielle ?

Pourquoi cela ne fonctionne pas ?

Les GML : Généralized Linear Models

Modèles linéaires généralisés

Visuellement

Les GML: Une généralisation

Les GML: Une généralisation

Mathématiquement…

La fonction de lien

Exemples de fonctions de lien courantes

La regession logistique

Classification binaire

Une première manière de voir les choses !

Visuellement

Regression logistique

Visuellement

Approche plus formelle…

Approche plus formelle…

En pratique

Modélisation

Qualité du modèle

Qualité du modèle

Prédiction

Faire des prédictions

Underfitting et Overfitting

Séparation des données

Entraînement vs Test

En pratique

Ce que ça donne

Entraînement du modèle

Prédictions sur le jeu de test

Prédictions avec probabilités

matrices de confusion

Comparaison

Courbes ROC

Courbes ROC - Comparaison

Références